The Shoulders Bear the World
By Carlos Drummond de Andrade
(Translated by Tony Marmo)
The shoulders bear the world,
There comes a time when one no more says ‘oh my God!’
A time of absolute purging,
When one no more says: ‘my love’,
For love turned out to be useless.
And the eyes don’t cry.
And the hands just perform the hard work.
And the heart is dry.
In vain women knock at your door, you will not open.
You ended up alone, the light is off,
but under the shadow your eyes shine enormous.
You are all certainty, you do not know how to suffer.
And from your friends you expect nothing.
What matter if old age comes: what is it after all?
Your shoulders bear the world
and it weighs no more than a child.
Wars, famine, arguments within buildings
only prove that life gos on
and not everyone has freed himself yet.
Some deem the show barbaric:
They (the frail people) prefer to die.
A time has come when death is useless.
When to live is an order.
Just live life, no mystification.
Maieutikos
vendredi, juin 22, 2007
lundi, novembre 06, 2006
AN ODE TO THANKLESSNESS
The following is a famous poem by Augusto dos Anjos, whereby he argues that, in order to survive, one needs to learn ungratefulness and retribution as a basic protection against both false friends and solitude.
It is considered one of the most eloquent poems of pessimism and reflects the personal unfortunate experiences the author had undergone in his life.
Private Verses
By Augusto dos Anjos
Translated from Portuguese by Tony Marmo
Lo! The awesome burial of thy last Chimaera none has attended.
Thy only inseparable companion has been this panther, Ingratitude!
Accustom thyself to the mud waiting for thee.
In this miserable world,
He, who among the beasts dwells,
Shall feel the urge to become a beast too.
Take thy match and light thy cigarette!
O friend, the kiss precedes the spit,
The same hand that fondles one will cast a stone!
If there is anyone who feels pity for thy wound;
Stone the evil hand that fondles thee;
Spit on the kissing mouth.
dimanche, septembre 17, 2006
AN OLD PHILOSOPHICAL PUZZLE BY DE CAMOENS
Love, Invisible Fire
[A Puzzle]
By Luis Vaz de Camoens
Translated from Portuguese by Tony Marmo
A flame burning in ways unseen is Love;
A wound aching imperceptibly;
A discontent form of contentment:
O, such excruciating a pain is love and yet it hurts not.
Love is more unwillingness than strong will;
It is a lonely walk among the cloud;
When utter happiness is never enough;
When one makes sure that it is in loosing that he shall gain.
Love means that by his own consent one is bound;
That the winner shall serve the vanquished,
That we are loyal to those who kill us.
Nevertheless, if love is so contrary to itself,
how can its favour in human hearts
cause such friendship?
mardi, septembre 12, 2006
A POEM BY MARIO DE ANDRADE
I am ten thousand million guys
By Mario de Andrade
Tanslation: Tony Marmo
I have ten thousand, I have ten thousand million personalities,
My feelings give re-birth to themselves incessantly;
O mirrors, O Pyrenees, O rednecks,
Should a god die, I shall buy another in a convenience store.
The best words I hug in my bed,
And my sighs are other guys’ violins;
And I walk on the land just like the man who secretly finds his own kisses in the corners, taxis and hotel rooms;
O yeah, I am so many, I am so many guys,
But one day I shall happen onto myself,
Be patient, short minded swallows,
For only the oblivion will provide an explanation,
And only then my soul will work as an abode.
samedi, juin 17, 2006
Propaedeutics: Algebra (2)
Still incompleteHEYTING ALGEBRA
The word Algebra has been taken from a famous book by Algorism, Hisab al-jabr w’al-muqabala, which roughly means the Science of the Reunion and the Opposition. From the phrase al-jabar (the reunion) comes the modern term ‘algebra’. In its current usages, nevertheless, the name 'Algebra' has different meanings and senses, depending on what field of inquiry is considered.
Algebra, generally speaking, can be defined as the study of certain structures consisting of a set and a collection of operations defined on the set which are required to conform to certain axioms. (Thus, a set itself is a degenerate algebraic structure, one with zero operations defined on it.) E.g.: A unary system is an instance of simple algebraic structure, for it is a set with a unary operation, a function S→S. A groupoid is a set with a single binary operation. A lattice is a set with two associative, (cf. [1]), commutative (cf. [2]), idempotent (cf. [5]) operations satisfying the absorption law (cf. [4]).
The name Algebra can also be applied to a certain kind of algebraic structures, such as an algebra over a set, which is a non-empty subset of the power set of a set S closed under the intersection and union of pairs of sets and under complements of individual sets. It can also refer to another kind of algebraic structure, namely a module or vector space together with a bilinear operation as multiplication (as in the sense of an algebra over a field and associative algebra).
Accordingly, different kinds of algebras or algebraic structures have been conceived in the Logical, Mathematical and Philosophical literature. In the following we shall examine the concept of Heyting algebra:
Let L be a set with two binary operations, ∨ and ∧. A Heyting algebra H is an algebraic structure <L,∨,∧> of type <2,2> such that the following axioms hold for all members a, b, and c of L: [1] Associativity
i. (a∨b)∨c=a∨(b∨c)
ii. (a∧b)∧c=a∧(b∧c)
[2] Commutativityi. a∨b=b∨a
ii. a∧b=b∧a
[3] Distributivityi.(a∧b)∨c=(a∧c)∨(b∧c)
ii. (a∨b)∧c=(a∨c)∧(b∨c)
[4] Absorptioni. (a∨b)∧a=a
ii. (a∧b)∨a=a
[5] Idempontencei. a∨a=a.
ii. a∧a=a
[6] The neutral elementi. The infimum has a neutral element, called 1 by convention;
ii. The supremum has a neutral element, called 0 by convention.
[7] Pseudo-complementation
For all a and b in H there is a greatest element x of H such that a∧x≤b
In other words x is the relative pseudo-complement of a in respect to b.
By [1], [2], [4] and [5], a Heyting algebra is clearly a bounded lattice, which is to say, an algebraic structure consisting of a lattice and neutral elements 0 and 1 for the two operations. In other words, a Heyting algrebra can be briefly described as a bounded lattice with a pseudo-complement.Complement and Pseudo-Complement
Given an element a in a lattice L with 0, a complement of a, if it exists, is defined as an element b∈L, such that a∧b=0 and a∨b=1.
Where a complement of an element exists, it might happen that it is not unique. For instance, in the middle row of the following diagram any two of the three elements are complements of the third:
Given the non-uniqueness issue, the pseudo-complement of an element is thereby defined. In such case, a∨b=1 does not hold.
Accordingly an element b of a lattice L is a pseudo-complement of a∈L if a∧b=0 for any e such that e∈a=0 implies that c≤b.
In other words, bis the maximal element in the set {c∈L such that c∧a=0}.
Should x*, the pseudo-complement of an element x, exist, then it is unique. Where x* is the pseudo-complement of x, it is not the case that x is also the pseudo-complement of x*. This fact can be represented by the diagram below: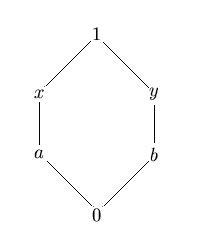
jeudi, juin 08, 2006
Collective violence is not for no good reason
OLIGANTHROPIA
Why so much violence? During the month of May, riots have taken place in several Brazilian prisons, were organised by a major criminal gang, whilst, at the same time, members of the same criminal gang, operating outside the prisons, engaged in systematic acts against civilians on the streets and in malls, perpetrating other crimes. This week, a peasant civil right movement tried to break into the House of Representatives in Brasilia and committed assault on the security agents of the Congress. These episodes of hysterical aggressiveness are never gratuitous: they are the reaction of a part of human population who has undergone greater violence.
So it does not matter whether it is Athens, Rome, Baghdad, Montreal, Rio de Janeiro or Sao Paulo: the war is on. Unlike in old Sparta and in present day Baghdad, the war is not by the wealthy aristocracy on the Eilotes or poor Arabians. But that was nothing new: during the month of may of this year of 2006, once again the Brazilian poor were channelling their anger in the wrong way against an establishment that feeds up on them, which has for years been shrinking the real purchase power of their wages by several means, increasing the taxes they pay, cutting their retirement pensions and taking their jobs out all at the same time.
Administration after administration, the self-proclaimed Nationalists, Conservatives, Liberals, Centrists, Moderate Leftists, Leftists and Marxists have been doing exactly the same: transferring income from the poor and the middle class to the already fat zillionaire financial portion of the elite. All of them have carrying out the same continued economic policies that cut investments in public sectors, concentrate income and consequently downgrades quality of life and worsen perspectives for the future. It is no exaggeration to say that the Military Regime was actually the Bankers’ rule, for no other sector of the economy has prospered more than them. After the re-democratisation of the country, civilian administrators have followed the same philosophy throughout more perverse and cynical methods, which made up the most fascist form of ideology called ‘neo-liberalism’ or simply the ‘financial market dictatorship’. Although all empirical evidences show that these policies produce nothing but disaster, and notwithstanding the arguments for these policies are mediocre, formally incorrect and inconsistent and immoral, the Nations’ leader cynically and arrogantly insist on them, mocking on others’ intelligence. Virtually all candidates, during their campaigns, admit that the economic policies are obviously criminal and dumb, but, shortly after they win elections, they change their speeches and start defending the visible massacre of their own constituents.
The scenes of extreme collective violence coordinated by the organised crime were clearly the logical result of dissatisfaction situation, where the angry masses were used and manipulated by unscrupulous gangsters, who are themselves both serial killers and mob bosses. That was the first incident of this type and magnitude in Sao Paulo though, it has already been the daily routine in Rio de Janeiro. The largest South American country has been in a state of civil war for decades: the only peculiar fact is that the rebels, who want vengeance against the moral, physical and economic violence they have undergone, have no true leadership to mobilise a concerted and effective action, and that is one of the main reasons the civil war has not ended yet.
,
lundi, mai 15, 2006
Propaedeutics: Algebra
Incomplete
L'Algèbre
L’Algèbre étude de certains ensembles sur lesquels on a mis une certaine structure, c’est voir dire, des ensembles munis d'une structure algébrique (groupes, anneaux, etc), indépendamment de leurs réalisations concrètes des propriétés, de la notion de limite (rattachée à l'analyse) et de la notion de représentation graphique (rattachée à la géométrie).
Une Algèbre sur un corps, ou autrement dit une K- algèbre se définit comme suit:
1. (E, +, •) est un espace vectoriel sur K
2. la loi × est définie de E x E dans E (loi de composition interne)
3. la loi × est distributive, à gauche et à droite, par rapport à la loi +
4. pour tout a, b dans K et pour tout x, y dans E alors (a•x)×(b•y) = (a×b)•(x×y)
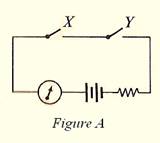
À l’aide d’un exemple des chaînes de contacts nous allons présenter une algèbre. Considérons la figure A où l’on distingue deux interrupteurs X et Y. Si X est ouvert et/ou si Y est ouvert, le courant ne passe pas. Le courant passe si ils sont fermés:
(...)
