Propaedeutics: Algebra (2)
Still incompleteHEYTING ALGEBRA
The word Algebra has been taken from a famous book by Algorism, Hisab al-jabr w’al-muqabala, which roughly means the Science of the Reunion and the Opposition. From the phrase al-jabar (the reunion) comes the modern term ‘algebra’. In its current usages, nevertheless, the name 'Algebra' has different meanings and senses, depending on what field of inquiry is considered.
Algebra, generally speaking, can be defined as the study of certain structures consisting of a set and a collection of operations defined on the set which are required to conform to certain axioms. (Thus, a set itself is a degenerate algebraic structure, one with zero operations defined on it.) E.g.: A unary system is an instance of simple algebraic structure, for it is a set with a unary operation, a function S→S. A groupoid is a set with a single binary operation. A lattice is a set with two associative, (cf. [1]), commutative (cf. [2]), idempotent (cf. [5]) operations satisfying the absorption law (cf. [4]).
The name Algebra can also be applied to a certain kind of algebraic structures, such as an algebra over a set, which is a non-empty subset of the power set of a set S closed under the intersection and union of pairs of sets and under complements of individual sets. It can also refer to another kind of algebraic structure, namely a module or vector space together with a bilinear operation as multiplication (as in the sense of an algebra over a field and associative algebra).
Accordingly, different kinds of algebras or algebraic structures have been conceived in the Logical, Mathematical and Philosophical literature. In the following we shall examine the concept of Heyting algebra:
Let L be a set with two binary operations, ∨ and ∧. A Heyting algebra H is an algebraic structure <L,∨,∧> of type <2,2> such that the following axioms hold for all members a, b, and c of L: [1] Associativity
i. (a∨b)∨c=a∨(b∨c)
ii. (a∧b)∧c=a∧(b∧c)
[2] Commutativityi. a∨b=b∨a
ii. a∧b=b∧a
[3] Distributivityi.(a∧b)∨c=(a∧c)∨(b∧c)
ii. (a∨b)∧c=(a∨c)∧(b∨c)
[4] Absorptioni. (a∨b)∧a=a
ii. (a∧b)∨a=a
[5] Idempontencei. a∨a=a.
ii. a∧a=a
[6] The neutral elementi. The infimum has a neutral element, called 1 by convention;
ii. The supremum has a neutral element, called 0 by convention.
[7] Pseudo-complementation
For all a and b in H there is a greatest element x of H such that a∧x≤b
In other words x is the relative pseudo-complement of a in respect to b.
By [1], [2], [4] and [5], a Heyting algebra is clearly a bounded lattice, which is to say, an algebraic structure consisting of a lattice and neutral elements 0 and 1 for the two operations. In other words, a Heyting algrebra can be briefly described as a bounded lattice with a pseudo-complement.Complement and Pseudo-Complement
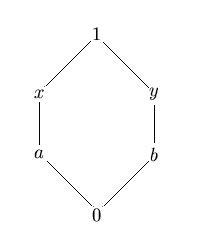
Given an element a in a lattice L with 0, a complement of a, if it exists, is defined as an element b∈L, such that a∧b=0 and a∨b=1.
Where a complement of an element exists, it might happen that it is not unique. For instance, in the middle row of the following diagram any two of the three elements are complements of the third:
Given the non-uniqueness issue, the pseudo-complement of an element is thereby defined. In such case, a∨b=1 does not hold.
Accordingly an element b of a lattice L is a pseudo-complement of a∈L if a∧b=0 for any e such that e∈a=0 implies that c≤b.
In other words, bis the maximal element in the set {c∈L such that c∧a=0}.
Should x*, the pseudo-complement of an element x, exist, then it is unique. Where x* is the pseudo-complement of x, it is not the case that x is also the pseudo-complement of x*. This fact can be represented by the diagram below: